![]()
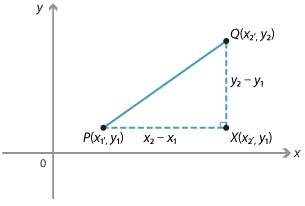
We can obtain a formula for the length of any interval. Suppose that \(P(x_1, y_1)\) and \(Q(x_2, y_2)\) are two points.
From the right-angled triangle \(PQX\), where \(X\) is the point \((x_2, y_1)\):
\(PX = x_2 - x_1\ \text{or}\ x_1 - x_2\ \text{and}\ QX = y_2 - y_1\ \text{or}\ y_1 - y_2\)
depending on the positions of P and Q.
By Pythagoras' theorem:
\begin{align}PQ^2 &= PX^2 + QX^2\\\\ &= (x_2 - x_1)^2 + (y_2 - y_1)^2.\end{align}Therefore \(\hspace{2em}PQ = QP = \sqrt{(x_2 - x_2)^2 + (y_2 - y_1)^2}\)
Note that \((x_2 - x_1)^2\) is the same as \((x_1 - x_2)^2\) and therefore it doesn't matter whether we go from \(P\) to \(Q\) or from \(Q\) to \(P\). The result is the same.